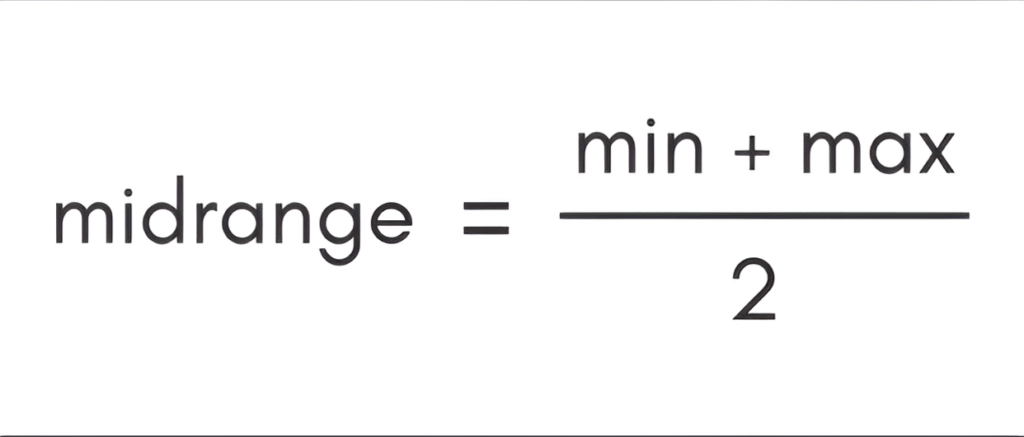The midrange is a simple measure of central tendency that represents the midpoint of a dataset in statistics. It is computed using the mean of the maximum and minimum values in the dataset. This provides a fast insight into the center of the dataset and can be useful alongside other measures such as the mean and median.
Calculating the Midrange
Calculating the Midrange
To compute, follow these steps:
- Identify the Maximum and Minimum Values: Determine the highest and lowest numbers in your dataset.
- Apply the Formula: Add the maximum and minimum values together and divide the sum by two.
- The formula is:
- Midrange=Maximum Value+Minimum Value/2
- The formula is:
Example Calculation
Consider the dataset: 10, 20, 30, 40, 50.
- Maximum Value: 50
- Minimum Value: 10
Applying the formula:
Midrange=50+102=602=30\text{Midrange} = \frac{50 + 10}{2} = \frac{60}{2} = 30Midrange=250+10=260=30
Thus, the midrange of this dataset is 30.
Calculating Midrange in Excel
Excel simplifies the midrange calculation with built-in functions:
Enter Your Data: Input your dataset into a single column or row.
Determine Maximum and Minimum Values:
Use the MAX function to find the highest value.
Use the MIN function to find the lowest value.
Compute the Midrange: Add the results of MAX and MIN, then divide by two.For example, if your data is in cells A1 through A5:
=MAX(A1:A5) returns the maximum value.
=MIN(A1:A5) returns the minimum value.
=(MAX(A1:A5) + MIN(A1:A5)) / 2 calculates the midrange.
Pros and Cons
The midrange is a fast way to get an estimate of the center of a dataset and is easy to compute. But it is very sensitive to exceptions, which can distort the result. As a result, it is most useful in conjunction with other measures of central tendency, such as the mean and median, and to get a complete picture of the data.